遇到(1+ax)^b*(1+cx)d/(1+e(x^f)^g 怎么求极限
1、当x趋近于无穷,求[(1+2x)^10*(1+3x)^20]/(1+6*x^2)^15的极限

2、首先我们看,他们都是高次带未知数的式子。并且是0/0型的
3、我们知道当x趋近于无穷,(3x^3+3x^2+3x)/(2x^3+2x^2+2x)=3/2。这个的解法是因为上下同时除了x^3
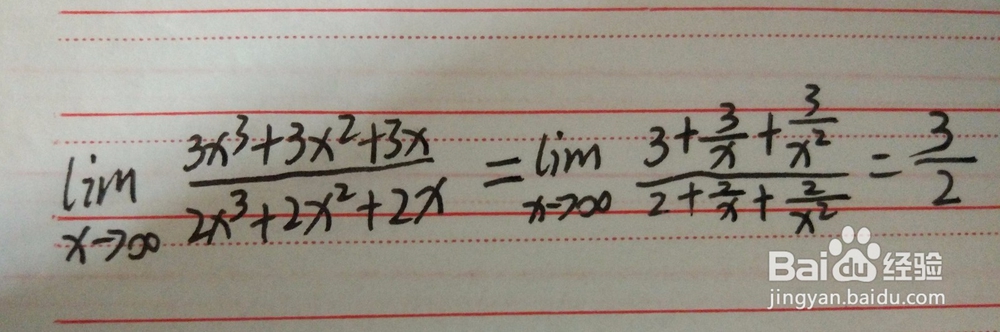
4、所以,由上面可以得到例题的求法就是最高次的系数之比[(2*x)^10*(3*x)^20]-------------------------(6x^2)^15得到极限为243/32
